The Features of 3.5: Post-quantum cryptography

This is the third in a series of posts about the features of OpenSSL 3.5. Its target audience is people who are curious about internet security, but who don’t recognize the acronyms in that list.

1. QUIC server
2. External QUIC library interface
3. Post-quantum cryptography

In order to explain “Hybrid ML-KEM in TLS v1.3” we need to start with the way internet security works today and how a new type of computer could change everything. The first post in this series introduced Transport Layer Security (TLS), which encodes messages sent across the internet. (v1.3 is the most recent version of the protocol.) Because of the way the internet works, you can’t necessarily control who can access the data you send and receive. Just as you lock your front door in order to keep strangers out, you need to encrypt messages to prevent strangers on the internet from reading them. In order to grant access to people you trust, you have to give them the key that opens the door.

When two computers connect with TLS, both sides of the connection agree on a secret key to lock subsequent messages. (This is part of the TLS handshake described in the previous post.) It’s no good just sending a key directly because the handshake messages can also be intercepted. That would be like leaving the key to your front door under the door mat. It won’t take long for people who want to get in to find that “secret” hiding place.

One solution is to use a key encapsulation mechanism (KEM). Instead of sending the key directly, this system sends the key using encryption that only the other party can read. In our Pi-day post about prime numbers we explained how this could be accomplished by multiplying two prime numbers to create a number called a public key. Anyone can use that number to encode messages that only the creator of the public key can read.

This is an asymmetric-key system because the public key locks messages in such a way that only the receiver, who has the matching private key, can unlock. The key sent by key encapsulation is called a symmetric key since the same key locks and unlocks all the messages. One might well ask why not use public keys to encode messages directly rather indirectly to send another key. The answer is that public key methods are inefficient compared to other methods.

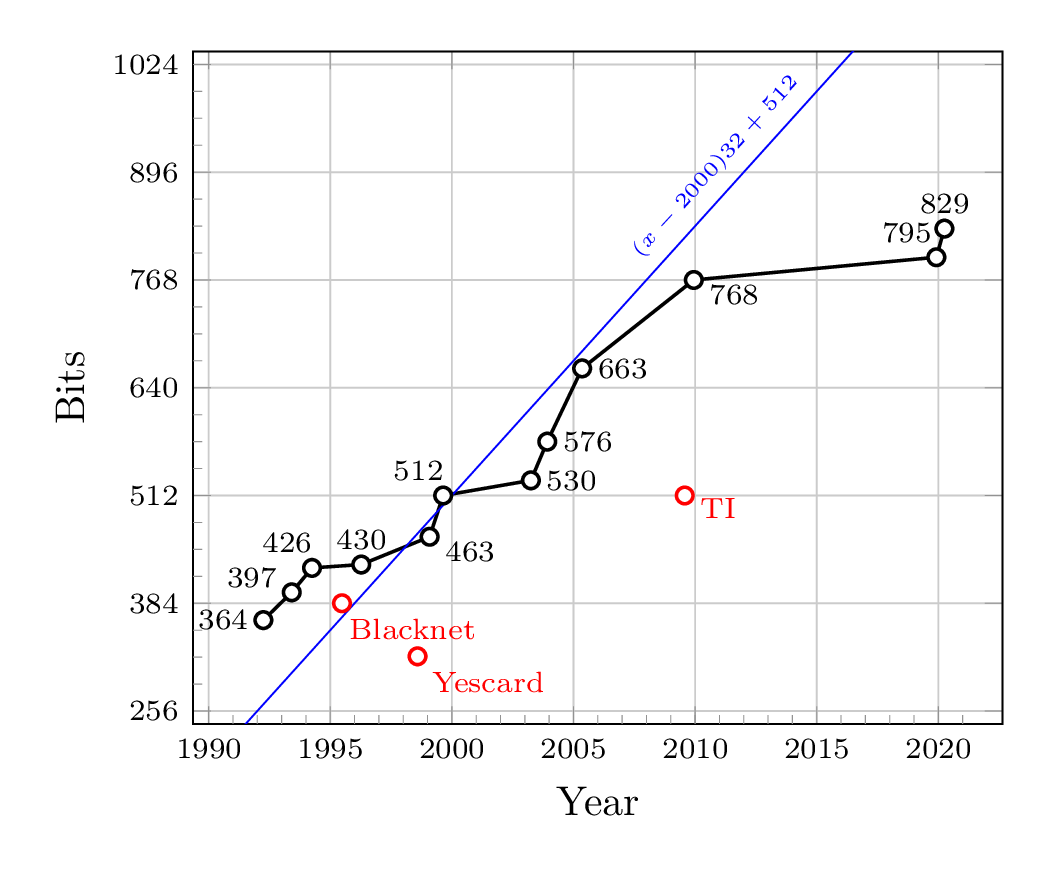
Our confidence in public keys based on factoring prime numbers (and similar one-way functions) depends on the reality that while computing power has been increasing steadily for many years, generating harder problems to solve is as simple as increasing the size of the keys we use. In 2020 researchers factored a 250 digit (829 bit) number using the equivalent of about 2700 years of computing on a single CPU core.¹ It was the largest known public key to be cracked.

By default, OpenSSL uses 2048 bit keys that take a fraction of a second to generate. The cost to break keys this size would be enormous and very few messages are worth the effort. The above graph shows RSA Challenge numbers in black and some of those challenges came with a prize for the team that cracked them. The red points represent keys that were used for protecting systems that hadn’t been updated for many years and had some value to the people who cracked them.² Ordinary internet traffic isn’t likely to be the target of this sort of attack and most messages would be long out-of-date by the time they are broken.

But what if there were a new type of computer that could quickly solve these sorts of problems? That is the promise of quantum computing. It might sound like an invention of science fiction, but companies such as Microsoft, IBM and Google have invested in hardware designed to take advantage of some strange characteristics of subatomic particles.

In classical computers, a bit stores information as either a 1 or a 0. A bit is physically represented by anything that has two distinct states: electrical switches, pulses of light, magnetic polarization, punch cards and so on. Over the last 50 years, technological innovation has found more and more ways to use the simple concept of bits to do all sorts of amazing things, including factoring large numbers.

Quantum computers use something called a qubit (“quantum bit”) to store information. Unlike a bit, a qubit can be somewhere on a spectrum between two states. Where a bit must be either 1 or 0, qubits only resolve to 1 or 0 (a “quantum state”) when observed. In a carefully controlled environment, it’s possible to manipulate qubits in a way that solves mathematical problems. Theoretically a quantum computer could factor current cryptographic keys in a fraction of the time it takes a classic computer to do the same thing.

The technology might be viable in a few years or it might take decades to perfect. At the moment there’s nothing to worry about for the vast majority of people who use the internet. But there is a risk, especially for data that has long-term value, that in a few years quantum computers could retroactively break into communication happening today and reveal sensitive or valuable information. There’s no time like the present for finding new ways to encrypt data so that we are ready for quantum computers.

Next time we’ll discus one solution to the problem.

Graph: fgrieu, CC BY-SA 4.0 via Cryptography Stack Exchange.